The Ising Model

The Ising model was introduced in the thesis of Ising, a German physicist (pronounciation: “easing”) and was intended as a simple model for ferromagnets.

Theory

It consists of spins that are either directed upwards or downwards and one interaction: Spins prefer to be aligned like their neighbouring spins. Each spin \(n_i\) from the set of all spins \(S\) has a set of neighbouring spins \(N_i\). Each spin has a value \(\pm 1\). The energy of the system is then defined as:

\[ E = \sum_{i\in S} \sum_{j\in N_i} S_i \cdot S_j\]

To get a simulation of this system Metropolis-Hastings Markov-chain Monte Carlo is used where the probability to be in a given configuration with an associated energy is given by the Boltzmann-distribution.

For further details about this consult the Wikipedia article.

Simulation

For my bachelor’s thesis “Sampling the Ising Model” in the laboratory “Scientific Computing” (supervised by Sabine Andergassen) I implemented the Ising model with Java and wrote a GUI with the processing library. The simulation featured single spin and cluster flip algorithms.

I later rewrote the simulation from my bachelor’s thesis in C# with a better GUI for the Campus Festival 2015 (650 year anniversary festival of the University of Vienna) where it was showcased as interactive nucleation simulation (pictured below).

The source code and binaries for both versions are available here

Readme

As I’ve recently came around to write a nice readme for the github repository I will just copy paste it here verbatim:

Ising Model

Two different implementations of the Ising Model - one with Java/Processing and one with C#/WPF. The Java version was used for my bachelor thesis, the C# version has more features and will be/was used for presentation on the Campus festival of the University of Vienna (June 2015, 650th year University of Vienna celebration).

Binaries are available under releases (for Windows only).

C#/WPF version:

Features

• Different color themes
• Simulation size can be changed while the simulation is running (spins will be scaled)
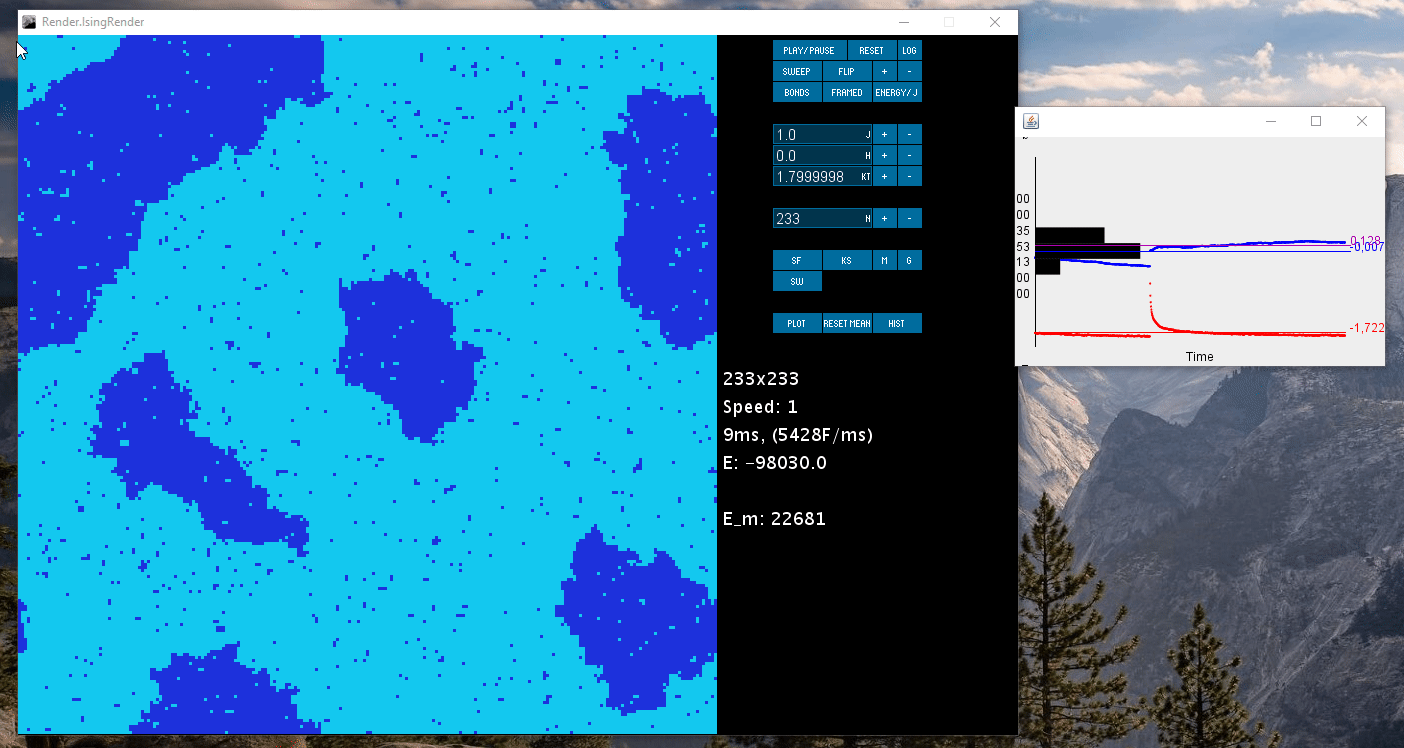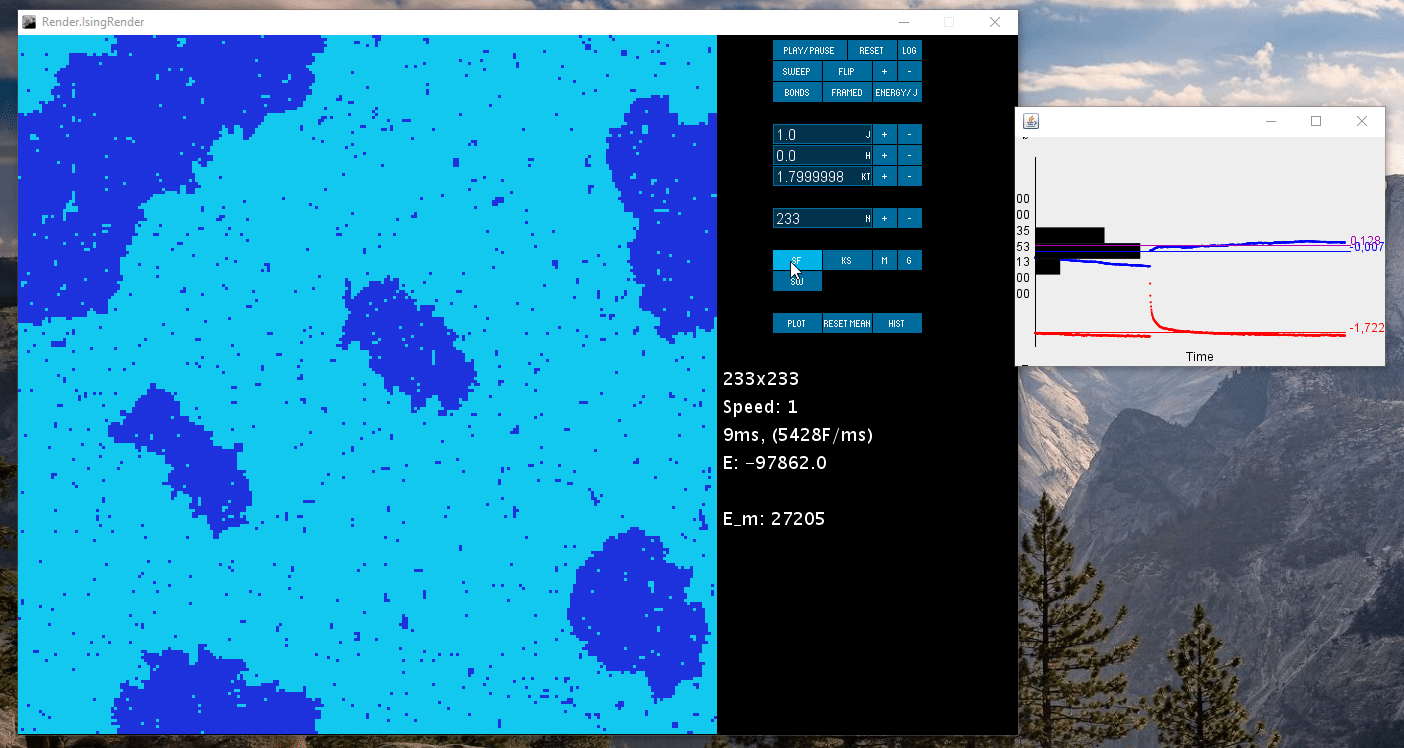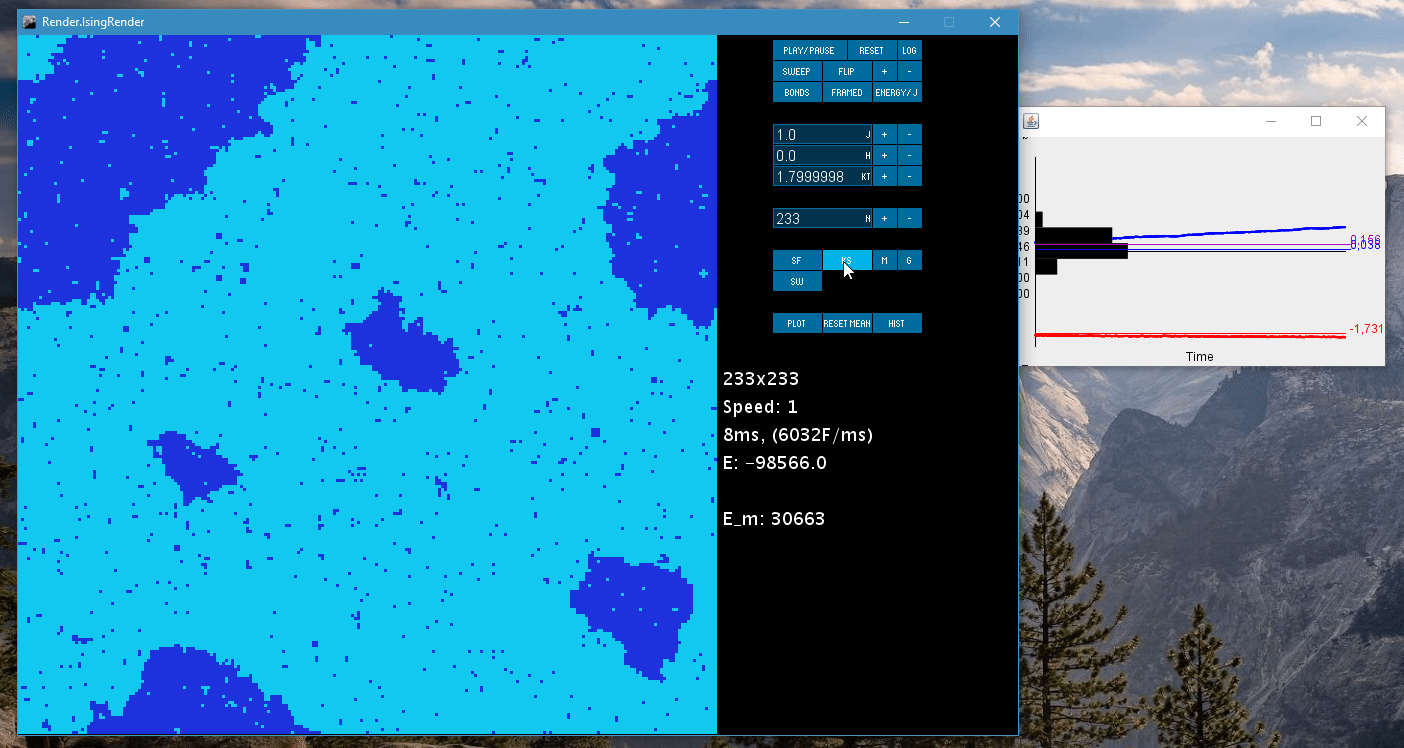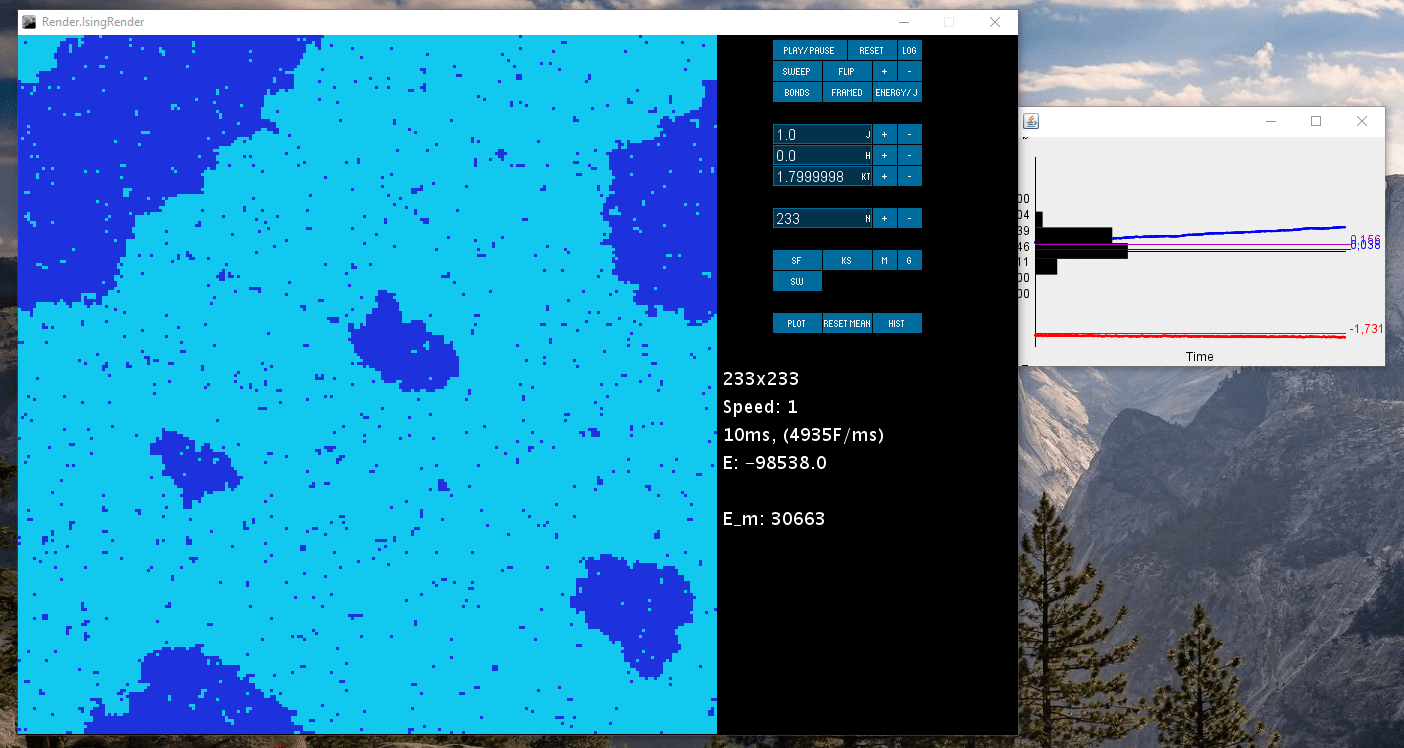
• Two different algorithms: Single spin flip metropolis hastings MCMC and spin preserving Kawasaki dynamics
• Coupling can be changed
• Real time plot of energy and magnetization
• Interactive simulation: Spins (or areas of spins) can be changed to face either up/down or to be non-interacting (left, middle, right mouse click, for all three: draw rectangle to select spins). The latter can be used to showcase heterogeneous nucleation (nucleation seeds form faster in pore-like structures, Frenkel 2006, Seeds of phase change, Page & Sear 2006, Heterogeneous Nucleation in and out of Pores)

Video

Java/Processing version:

Features:

• Simulation size can be changed
• Speed can be adapted (omit rendering of frames to produce data faster)
• Log data for further analysis
• Three algorithms: The two mentioned above as well as Swendsen-Wang cluster flip algorithm (removes auto-correlation from magnetization)
• Real time plotting (though ugly)

Video

Remarks

• Swendsen Wang implementation (in the Java version) uses a recursive depth first search for the cluster finding algorithm. If the simulated lattice has more than 20k spins this can lead to a StackOverflowException. Change the stacksize for the Java JVM to circumvent this.

• The C# version should overall be more performant, though it currently lacks options to set the simulation speed as it was programmed as an interactive showcase for kids during a science festival and not for getting simulation data. If you need this you’ll have to do it on your own.